"Pedal turn" versus "Conventional turn"
- Elite 1K
- Posts: 1047
- Joined: 17 Oct 2010, 19:10
viewtopic.php?f=22&t=52907
Now we know the "pedal turn", is a high yaw rate maneuver, not a conventional turn. So it is neither sustained turn, nor instantaneous turn. However, since the angular velocity (28 deg/sec) is constant, pedal turn is equivalent to a sustained turn of 28 deg/sec, because it changes its heading at a steady 28deg/sec, and an enemy fighter could not counter it unless it performs a sustained 28deg/sec turn (conventionally or yawing).
Is this understanding correct?
Now we know the "pedal turn", is a high yaw rate maneuver, not a conventional turn. So it is neither sustained turn, nor instantaneous turn. However, since the angular velocity (28 deg/sec) is constant, pedal turn is equivalent to a sustained turn of 28 deg/sec, because it changes its heading at a steady 28deg/sec, and an enemy fighter could not counter it unless it performs a sustained 28deg/sec turn (conventionally or yawing).
Is this understanding correct?
Last edited by gta4 on 03 Apr 2017, 02:27, edited 1 time in total.
- Active Member
- Posts: 159
- Joined: 10 Jul 2016, 15:27
The pilot is just stomping on one of the pedals, right? It's not a banked turn. That means that the plane is having to generate the centripetal force more or less just with the vertical surfaces. The tail surfaces are a whole lot smaller than the wings, so the airfoils used to perform this maneuver are going to be very heavily loaded. I would be pretty dubious that it's "sustained" in the sense that the aircraft isn't losing energy.
- Elite 1K
- Posts: 1047
- Joined: 17 Oct 2010, 19:10
Dragon029 wrote:Yes, but pedal turns aren't as flexible / as versatile as performing a conventional turn - you can't perform them at as fast an airspeed
So F-35 could just perform the conventional turn first and let the speed bleed to an appropriate value to execute the pedal turn. The total angle of turning is sufficient for a missile shot?
Last edited by gta4 on 03 Apr 2017, 13:27, edited 1 time in total.
- Elite 1K
- Posts: 1047
- Joined: 17 Oct 2010, 19:10
collimatrix wrote:The pilot is just stomping on one of the pedals, right?
Not really. It also involves the proverse yaw effect from the differential deflection of ailerons, and in fact most of the turning torque comes from the aileron, not the rudders:
viewtopic.php?f=22&t=52503&p=356317&sid=2dd6609c08b03020804a6283d4e6020c#p356317
"At low AOA, rudder is responsible for yaw, while aileron is responsible for roll. Pedal input only causes rudder to deflect."
"But at high AOA it's the other way round. Rudder has more roll authority while aileron has more yaw authority. So at the presence of an abrupt pedal input, modern flight control software will interpret it as a yaw command and deflect both aileron and rudder, where most of the turning (yaw) torque is actually from the aileron. The rudder in this case is a stabilizer that prevent the aircraft from departure."
"F-35 has a very big aileron/wing area ratio. That is probably the reason for which it could generate so much turning torque, and to make that 28 deg/sec turn constant. Rudder can not make that rate sustainable because it loses controllability at high angle of sideslip."
gta4 wrote:Dragon029 wrote:Yes, but pedal turns aren't as flexible / as versatile as performing a conventional turn - you can't perform them at as fast an airspeed
So F-35 could just perform the conventional turn first and let the speed bleed to an appropriate value to execute the pedal turn. The total angle of turning is sufficient for a missile shot.
Potentially, but there's scenarios where they won't get the chance to do that; an F-15 or equivalent might be wary of the F-35's low airspeed manoeuvring capability and decide to immediately go vertical after the merge. If that happens and the F-35 pilot made the mistake of turning level or downward, they won't get the chance to use the pedal turn, not unless the F-15, etc fails to kill the F-35 when it dives back down, at which point the F-35 might be able to give chase down low and put them on the defensive (depending on how far the F-15 can get before it has to pull up and shred energy).
Don't get me wrong, it'll definitely be useful at times and be the decisive manoeuvre in some fights, but if a pilot had a choice between a sustained 28 deg/s pedal turn vs a sustained 28 deg/s pitching turn rate, they'd definitely pick the latter.
- Active Member
- Posts: 159
- Joined: 10 Jul 2016, 15:27
gta4 wrote:collimatrix wrote:The pilot is just stomping on one of the pedals, right?
Not really. It also involves the proverse yaw effect from the differential deflection of ailerons, and in fact most of the turning torque comes from the aileron, not the rudders:
viewtopic.php?f=22&t=52503&p=356317&sid=2dd6609c08b03020804a6283d4e6020c#p356317
"At low AOA, rudder is responsible for yaw, while aileron is responsible for roll. Pedal input only causes rudder to deflect."
"But at high AOA it's the other way round. Rudder has more roll authority while aileron has more yaw authority. So at the presence of an abrupt pedal input, modern flight control software will interpret it as a yaw command and deflect both aileron and rudder, where most of the turning (yaw) torque is actually from the aileron. The rudder in this case is a stabilizer that prevent the aircraft from departure."
"F-35 has a very big aileron/wing area ratio. That is probably the reason for which it could generate so much turning torque, and to make that 28 deg/sec turn constant. Rudder can not make that rate sustainable because it loses controllability at high angle of sideslip."
Aha, thank you.
So it's a low-speed, high-AOA maneuver?
- Elite 1K
- Posts: 1047
- Joined: 17 Oct 2010, 19:10
Dragon029 wrote:gta4 wrote:Dragon029 wrote:Yes, but pedal turns aren't as flexible / as versatile as performing a conventional turn - you can't perform them at as fast an airspeed
So F-35 could just perform the conventional turn first and let the speed bleed to an appropriate value to execute the pedal turn. The total angle of turning is sufficient for a missile shot.
Potentially, but there's scenarios where they won't get the chance to do that; an F-15 or equivalent might be wary of the F-35's low airspeed manoeuvring capability and decide to immediately go vertical after the merge. If that happens and the F-35 pilot made the mistake of turning level or downward, they won't get the chance to use the pedal turn, not unless the F-15, etc fails to kill the F-35 when it dives back down, at which point the F-35 might be able to give chase down low and put them on the defensive (depending on how far the F-15 can get before it has to pull up and shred energy).
Don't get me wrong, it'll definitely be useful at times and be the decisive manoeuvre in some fights, but if a pilot had a choice between a sustained 28 deg/s pedal turn vs a sustained 28 deg/s pitching turn rate, they'd definitely pick the latter.
Thanks. That clears it all.
- Senior member
- Posts: 457
- Joined: 21 Mar 2008, 04:40
https://www.youtube.com/watch?v=NW0wKltGGaE
At mark :35 as the F-22 rolls out of a high energy, high banked turn where there is little if any unloading as it pitch, rolls and yaws? I imagine a rolling scissors situation where the F-22/35 could yank on the stick and stomp on the pedal and achieve a quick nose on target maneuver without losing to much energy like we see in the pirouette. The FCS on modern AC should allow the pilot to put the AC into whatever position and the FCS does the rest. So if a pilot wishes to keep his energy up and roll out of a banking turn the AC will let him or if the pilot gets stuck in a low energy nose pointing battle it will do that also.
At mark :35 as the F-22 rolls out of a high energy, high banked turn where there is little if any unloading as it pitch, rolls and yaws? I imagine a rolling scissors situation where the F-22/35 could yank on the stick and stomp on the pedal and achieve a quick nose on target maneuver without losing to much energy like we see in the pirouette. The FCS on modern AC should allow the pilot to put the AC into whatever position and the FCS does the rest. So if a pilot wishes to keep his energy up and roll out of a banking turn the AC will let him or if the pilot gets stuck in a low energy nose pointing battle it will do that also.
You can't shot what you can't see - Unknown
- Elite 3K

- Posts: 3906
- Joined: 16 Feb 2011, 01:30
"So it's a low-speed, high-AOA maneuver?"
Always.
Always.
Has it been determined / verified / concluded that the pedal turn is another name for a J-turn or Herbst maneuver?
Take an F-16, stir in A-7, dollop of F-117, gob of F-22, dash of F/A-18, sprinkle with AV-8B, stir well + bake. Whaddya get? F-35.
- Elite 5K

- Posts: 6009
- Joined: 10 Mar 2006, 01:24
- Location: Nashua NH USA
steve2267 wrote:Has it been determined / verified / concluded that the pedal turn is another name for a J-turn or Herbst maneuver?
I honestly think of it more like the helicopter turn the F-22 does, right or wrong. Hit ~45 AoA, stomp pedal, the nose slices around while the flight path is ballistic.
"Spurts"
-Pilot
-Aerospace Engineer
-Army Medic
-FMS Systems Engineer
-PFD Systems Engineer
-PATRIOT Systems Engineer
-Pilot
-Aerospace Engineer
-Army Medic
-FMS Systems Engineer
-PFD Systems Engineer
-PATRIOT Systems Engineer
sprstdlyscottsmn wrote:steve2267 wrote:Has it been determined / verified / concluded that the pedal turn is another name for a J-turn or Herbst maneuver?
I honestly think of it more like the helicopter turn the F-22 does, right or wrong. Hit ~45 AoA, stomp pedal, the nose slices around while the flight path is ballistic.
I think we don't know what we don't know, unless PIL pigeonholes another Lightning rider at an airshow, or someone gets to converse with Beasley, Dolby, Mau, Berke or ... and ask them specifics.
In another thread, JohnWill I think it was, commented that at high AoA (e.g. 45°), left/right stick commands roll around the aircraft flight or velocity vector. Such a roll will be a combination of body-axis roll and yaw. Trying to visualize this some more, it is not clear to me if stomping on the left / right rudder pedals at 45° AoA will be a pure body-axis roll as at 0° AoA, but I think it will be. (For example, at 0° AoA, pure body-axis yaw results in no change in angle-of-attack. At 90°, pure body-axis yaw also does not change alpha. That is, (body-axis) yaw 90° left or right at 90° AoA, and you are still at 90°alpha. But I may need to think about this some more.)
So... it seemed to me, if one commanded a large roll at high alpha, and supplemented that roll with a firm push on the accompanying rudder pedal (i.e. left roll + left rudder pedal), you would generate a left roll plus lots of left yaw. And the resulting maneuver would seem to be very similar to illustrations of the Herbst maneuver performed by the X-31 and the NASA F-18. (Since it is high-alpha capable as well, perhaps the F/A-18 can perform a similar maneuver? The F-35 has, after all, been described as an F/A-18 with "four engines" or "with a turbo".)
Take an F-16, stir in A-7, dollop of F-117, gob of F-22, dash of F/A-18, sprinkle with AV-8B, stir well + bake. Whaddya get? F-35.
A new reader to this thread, unfamiliar with the "pedal turn", may do well to read the thread, What is the pedal turn that generates a constant 28deg/sec?.
From my post viewtopic.php?p=356498#p356498 in that thread, if the "pedal turn" is a Herbst maneuver, then these illustrations may help the reader visualize the maneuver, and perhaps give some idea of the tactical significance such a capability provides.
It appears that the Herbst maneuver is also used in an offensive spiral.


The NASA F-18 HARV program in 1983 also seems relevant: https://www.nasa.gov/centers/dryden/his ... RV/rd.html


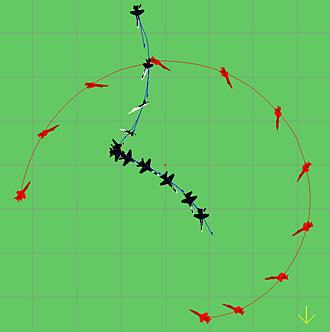
From my post viewtopic.php?p=356498#p356498 in that thread, if the "pedal turn" is a Herbst maneuver, then these illustrations may help the reader visualize the maneuver, and perhaps give some idea of the tactical significance such a capability provides.
It appears that the Herbst maneuver is also used in an offensive spiral.


The NASA F-18 HARV program in 1983 also seems relevant: https://www.nasa.gov/centers/dryden/his ... RV/rd.html



Take an F-16, stir in A-7, dollop of F-117, gob of F-22, dash of F/A-18, sprinkle with AV-8B, stir well + bake. Whaddya get? F-35.
steve2267 wrote:In another thread, JohnWill I think it was, commented that at high AoA (e.g. 45°), left/right stick commands roll around the aircraft flight or velocity vector. Such a roll will be a combination of body-axis roll and yaw. Trying to visualize this some more, it is not clear to me if stomping on the left / right rudder pedals at 45° AoA will be a pure body-axis roll as at 0° AoA, but I think it will be. (For example, at 0° AoA, pure body-axis yaw results in no change in angle-of-attack. At 90°, pure body-axis yaw also does not change alpha. That is, (body-axis) yaw 90° left or right at 90° AoA, and you are still at 90°alpha. But I may need to think about this some more.)
Usually, roll axis control variable LCV is stability-axis roll rate at normal and high dynamic pressures. Stability axis roll rate is
Ps = Pb * cos(α) + Rb * sin(α)
where Pb and Rb are body-axis roll and yaw rate, respectively. The reason Ps is used as LCV instead of Pb is that at AoA rolling about the body axis converts α to β. E.g., if I roll 90° around the body x-axis at 20° α, I now have 20° β and 0° α. Since we want to maintain the current angle-of-attack and coordinated flight (i.e., β small) we roll about the stability-axis.
At low dynamic pressures, LCV is Pb because at low speeds because it is less desirable to roll around the velocity vector and because at low qbar the incidence angles (α and β) become difficult to measure and can also become undefined.
The yaw control variable NCV is Rb at low qbar and is a mix of Rs = Rb * cos(α) - Pb * sin(α), β feedback, and decoupling terms at high qbar. The goals are to
- maintain zero steady-state lateral acceleration with no pedal input (i.e. coordinated flight)
- achieve a satisfactory response of sideslip and Rs with pedal input.
Based on AIAA 2002-6020, NCV for the X-35B in non-hover mode is
NCV = Rb * cos(α) - Pb * sin(α) - g/V * sin(φ) * cos(θ).
"You could do that, but it would be wrong."
Who is online
Users browsing this forum: No registered users and 7 guests